优化设计的基本术语和数学模型
优化设计方法是一种规格化的设计方法,它首先要求将设计问题按优化设计所规定的格式建立数学模型,选择合适的优化方法及计算机程序,然后再通过计算机的计算,自动获得最优设计方案。
工程设计问题的优化,可以表达为优选一组参数,使其设计指标达到最佳值,且须满足一系列对参数选择的限制条件。这样的问题在数学上可以表述为:在以等式或不等式表示的约束条件下求多变量函数的极小值或极大值问题,即求:
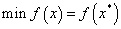
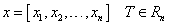
受约束于:
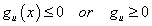
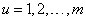
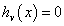
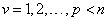
因此,优化设计都应按此形式将工程设计问题作出数学上的描述,适应采用优化设计方法求解的需要,这就是所谓优化设计的数学模型。下面首先介绍优化设计中常用的几个基本术语。
1. 设计变量
在工程设计中,区别不同的设计方案,通常是以一组取值不同的参数来表示。这些参数可以是表示构件形状、大小、位置等的几何量,也可以是表示构件质量、速度、加速度、力、力矩等的物理量。
在构成一项设计方案的全部参数中,可能有一部分参数根据实际情况预先确定了数值,它们在优化设计过程中始终保持不变,这样的参数称为给定参数。另一部分参数则是需要优选的参数,它们的数值在优化设计过程中是变化的,这类参数称为设计变量,它们相当于数学上的独立自变量。
一个优化设计问题如果有n个设计变量,而每个设计变量用xi(i=1,2,…,n)表示,则可以把n个设计变量按一定的次序排列起来组成一个列阵或行阵的转置:
我们把X定义为n维欧氏空间的一个向量,设计变量x1,x2,…,xn为向量X的n个分量。在优化设计中把这个n维的欧氏实空间称为设计空间,用Rn表示,它是以设计变量x1,x2,…,xn为坐标轴的n维空间。设计空间包含了该项设计所有可能的设计方案,且每个设计方案就对应着设计空间一个设计向量或者说一个设计点X。
设计变量的数目越多,其设计空间的维数越高,能够组成的设计方案的数量也就越多,因而设计的自由度也就越大,从而也就增加了问题的和复杂程度。一般来说,优化设计过程的计算量是随设计变量数目的增多而迅速增加的。因此,对于一个优化设计问题来说,应该恰当地确定设计变量的灵敏度。并且原则上讲,应尽量减少设计变量的数目,即尽可能把那些对设计指标影响不大的参数取作给定参数,只保留那些对设计指标影响显著的、比较活跃的参数作为设计变量,这样可以使优化设计的数学模型得到简化。
设计变量通常是有取值范围的,即:
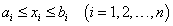
式中:ai、bi分别表示设计变量xi的下界约束值和上界约束值。在设计变量的取值范围中,设计变量的取值多数是连续的,但有些设计变量只能选用规定的离散值。
对于有离散型设计变量的优化设计问题,有两种处理方法:一是先按连续型设计变量对待进行求解,然后再对最优解进行离散化后处理,但是离散化后处理有时会使结果远离最优解;另一是选用能处理离散型设计变量的优化设计方法进行求解,但这些方法种类较少,且求解能力较弱。
2. 目标函数
每一个设计问题,都有一个或多个设计中所追求的目标,它们可以用设计变量的函数来加以描述,在优化设计中称它们为目标函数。当给定一组设计变量值时,就可计算出相应的目标函数值。因此,在优化设计中,就是用目标函数值的大小来衡量设计方案的优劣的。
优化设计的目的就是要求所选择的设计变量使目标函数值达到最佳值。最佳值可能是极大值,也可能是极小值,由于求目标函数f(x)的极大化等价于求目标函数―f(x)的极小化,因此,为算法和程序的统一,通常最优化就是指极小化,即f(x)→min。
在工程设计问题中,设计所追求的目标可能是各式各样的,当目标函数只包含一项设计指标极小化时,称它为单目标设计问题。当目标函数包含多项设计指标极小化时,这就是所谓的多目标设计问题。
单目标优化设计问题,由于指标单一,易于衡量设计方案的优劣,求解过程比较简单明确。而多目标问题则比较复杂,多个指标往往构成矛盾,很难或者不可能同时达到极小值。多目标问题的求解,较为简单的方法是采用线性加权的和的形式将多目标问题转为一个单目标问题求解,或将一些目标转为约束函数。这样处理后的数学模型,往往不能很好地体现多目标问题的实质,求得的最优解不能很好地满足设计要求。
由于目标函数是设计变量的函数,故给定一组设计变量值就相应地有一个函数值,并在设计空间相对应地有一个设计点,因此也可以说设计空间的任何一点都有一个函数值与之相对应。具有相同函数值的点集在设计空间内形成一个曲面或曲线,称为目标函数的等值面或等值线。
在优化设计中正确建立目标函数是很重要的一步工作。它不仅直接影响到优化设计的质量,而且对整个优化计算的繁简难易也会有一定的影响。还有,并不是所有优化设计问题的目标都可以用显式的目标函数来描述,如:原理方案设计、下料问题等。
3. 设计约束
优化设计不仅要使所选择方案的设计指标达到最佳值,同时还必须满足一些附加的条件,这些附加的设计条件都是对设计变量取值的限制,在优化设计中叫做设计约束。它的表现形式有两种,一种是不等式约束,即:
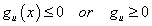
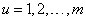
另一种是等式约束,即
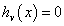
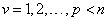
式中,gu(x)和hv(x)分别为设计变量的函数,统称为约束函数;m和p分别表示不等式约束和等式约束的个数,而且等式约束的个数p必须小于设计变量的个数n。因为从理论上讲,存在一个等式约束就可以用它消去一个设计变量,这样便可降低优化设计问题的维数。
根据约束的性质不同,可以将设计约束分为区域约束和性能约束两类。所谓区域约束是直接限定设计变量取值范围的约束条件;而性能约束是由某些必须满足的设计性能要求推导出来的约束条件。在求解时,对这两类约束有时作不同的对待。
不等式约束及其有关概念,在优化设计中是相当重要的。每一个不等式约束都把设计空间划分成两部分,一部分是满足该不等式约束条件的,另一部分则不满足。两部分的分界面叫做约束面。一个优化设计问题的所有不等式约束的边界将组成一个复合约束边界,复合边界内的区域是满足所有不等式约束条件的部分,在这个区域中所选择的设计变量是允许采用的,这个区域称为设计可行域或简称可行域。除去可行域以外的设计空间称为非可行域。
据此,在可行域内的任一设计点都代表了一个允许采用的设计方案,这样的点叫做可行设计点或内点。在约束边界上的点叫做极限设计点或边界点,此时这个边界所代表的约束叫做适时约束或起作用约束。
在建立数学模型时,目标函数与约束函数不是绝对的。对于同一对象的优化设计问题(如齿轮传动优化设计),不同的设计要求(如要求重量最轻或承载能力最大等),反映在数学模型上是选择不同的目标函数和约束函数,设定不同的约束边界值。
换言之,目标函数和约束函数都是设计问题的性能函数,只是在数学模型中充当不同的角色。所以,通常的做法是将目标函数和约束函数视为问题函数,建立起某一对象的优化设计通用数学模型,求解时,再根据具体的设计要求,指定某个或某些问题函数为目标函数,某些问题函数为约束函数且设定边界值。
当优化数学模型中的问题函数均为设计变量的线性函数,则称为线性规划问题。若问题函数中包含非线性函数时,则称为非线性规划问题。多数工程优化设计问题的数学模型是属于有约束的非线性规划问题。
4. 约束优化设计问题的最优解
优化设计就是求解n个设计变量在满足约束条件下使目标函数达到最小值,即:
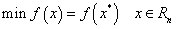
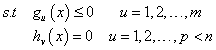
式中,称x*为最优点,称f(x*)为最优值。最优点x*和最优值f(x*)即构成了一个约束最优解。
在约束优化设计问题中,如果目标函数是多峰的,或约束集合是非凸集,则有可能存在不止一个局部极小点,此时每一个局部极小点和对应的局部极小值统称为一个局部最优解。
显然,我们总是期望获得全域最优解,但一般情况下是很难断定所得的一个解就是全域最优解。在优化设计求解过程中,绝大多数的是优化方法都是通过参照当前点周围的信息来判断是否找到了最优解,这样求得的解很可能是局部最优解,不同的初始点可能求得不同的最优解。
所以,在求解约束优化设计问题时,通常的做法是用多个方法程序、多个初始点来求同一个问题,再从求得的多个局部最优解中取一个最优的。
建筑资质代办咨询热线:13198516101

 咨询热线:13198516101
咨询热线:13198516101 
