功率谱密度(功率信号)和能量谱密度(能量信号)
能量信号和功率信号1
根据信号可以用能量式或功率式表示可分为能量信号和功率信号。
能量信号:如各类瞬变信号
在非电量测量中,常将被测信号转换为电压或电流信号来处理。显然,电压信号加在单位电阻(R=1时)上的瞬时功率为:

瞬时功率对时间积分即是信号在该时间内的能量。通常不考虑量纲,而直接把信号的平方及其对时间的积分分别称为信号的功率和能量。当x(t)满足:
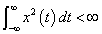
则信号的能量有限,称为能量有限信号,简称能量信号。满足能量有限条件,实际上就满足了绝对可积条件。
我们定义信号f(t)的能量(作用归一化处理):由电压f(t)(或者电流在1Ω电阻上消耗的能量):
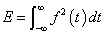
注释:
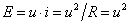
功率信号:如各种周期信号、常值信号、阶跃信号等。
若x(t)在区间(-∞,∞)的能量无限,不满足能量有限信号条件,但在有限区间(-T/2,T/2)满足平均功率有限的条件:
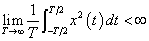
我们定义信号f(t)的平均功率,为电压f(t)在1Ω电阻上消耗的平均功率(简称功率):

频谱和频谱密度2
频谱密度:设一个能量信号为s(t),则它的频谱密度S(w)可以由付氏变换求得。

能量信号的频谱密度S(f)和功率信号C(jnw)(比如一个周期信号)的频谱主要区别有:
-
S(f)是连续谱,而C(jnw)是离散谱;
-
S(f)单位是幅度/频率,而C(jnw)单位是幅度(这里都是指其频谱幅度);
-
能量信号的能量有限,并连续的分布在频率轴上,每个频率点上的信号幅度是无穷小的,只有df上才有确定的非0振幅。
功率信号的功率有限,但能量无限,它在无限多的离散频率点上有确定的非0振幅。
以下为推导过程:
由周期信号推导非周期信号的频谱(频谱密度):
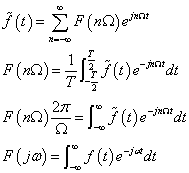
由上面可以看书,F(jω)是一个谱密度函数,它的实际幅度是F(nΩ),是个无穷小量,但是F(nΩ)*2π/Ω以无穷小/无穷小得到一个常量,单位是幅度/频率。并且:
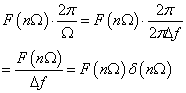
在频域上积分就是其频谱幅度。同时,周期信号有:
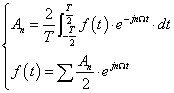
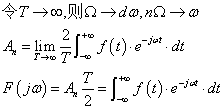
其中:
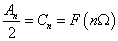
Cn是以e∧jnΩt为基底的系数。
功率谱(密度)与能量谱(密度)3
功率谱:也称功率谱密度(PSD),单位是功率/Hz。针对功率有限信号的(能量有限信号用能量谱密度),所表现的是单位频带内信号功率随频率的变换情况。
能量谱:也叫能量谱密度,单位是焦耳/Hz。针对能量有限的信号,能量信号傅里叶变换绝对值的平方就是能量谱(密度)【帕塞瓦尔定理】。
功率谱针对能量无限(功率有限)的功率信号,功率信号不满足傅里叶变换的绝对可积的条件,其付里叶变换是不存在的,如正弦函数的付里叶变换是不存在,只有引入了冲激函数才求得其付里叶变换。功率谱不能直接进行傅立叶变换,通常使用短截函数进行截取后,如图:
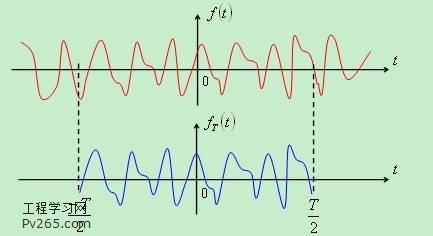
使用时间T进行短截原来的信号,当T->无穷大时:
设FT(ω)为fT(t)的傅里叶变换,根据帕塞瓦尔定理,fT(t)的能量ET是:
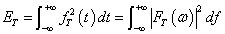
其中能量谱密度G(f)表示为:
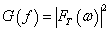
故平均功率为:
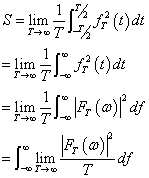
其中:(平均)功率谱密度为:
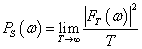
这是对模拟信号的时域计算方法,当进行AD采样,变为数字信号后,宜根据下文计算方法求功率谱。
功率谱计算公式4
周期图法:它是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅立叶变换,得X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计。
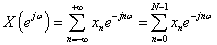
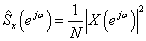

自相关法: 根据维纳-辛钦定理,先估计相关函数,再经傅立叶变换得功率谱估计。
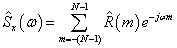
功率谱与自相关函数是一个傅氏变换对。功率谱具有单位频率的平均功率量纲,所以标准叫法是功率谱密度。通过功率谱密度函数,可以看出随机信号的能量随着频率的分布情况。像白噪声就是平行于w轴,在w轴上方的一条直线。
能量信号频谱通常既含有幅度也含有相位信息;傅里叶变换幅度谱的平方(二次量纲),又叫能量谱(密度),它描述了信号能量的频域分布;功率信号的功率谱描述了信号功率随频率的分布特点,也已证明,信号功率谱恰好是其自相关函数的傅氏变换。

本文来源于新浪博客LAY1984_XL的博客。
建筑资质代办咨询热线:13198516101

 咨询热线:13198516101
咨询热线:13198516101 
